Diagram

[ecmoloney]

This bread game went very slowly for me! Can someone please post their diagram? Thanks.

[aileenann]

This is a tough one to diagram, and I think there could be more than one way to do it. I treated this like an open assignment board, although I did not find too many inferences because there does not seem to be very much predetermined by the constraints. What do you think? Any suggestions to improve my diagram?

[bergstressers]

This one seemed too open at first so in the interest of time I just gave up on diagramming and jumped into the questions, which (atypically) worked well even beyond the just-apply-the-given-rules-until-only-one-is-left question. The answers to all the questions except for 2 shake out directly from the initial rules, no inference needed.

[aileenann]

Thanks for the tip!

It's good to know that some games (and really all games, if you get right down to it, can be done without a diagram, but darn it, sometimes that can take a long time. I'd say the best bet is to try your best at the diagram *always* but don't forget that you can always fall back on the constraints themselves if you can't produce a diagram or if your diagram is not very helpful.

[savannajolie]

Hi All,

Quick question- the answer to number 2 is A because:

the answer calls for only three oatmeal cookies and that would break the last rule that states "If two or more of the loaves are unsliced, then at lease one of the unsliced is rye."The answer calls to have just three Oatmeals to be unsliced leaving the remaining rye slices to be sliced. This is a must be false.

[aileenann]

Yes, that is exactly the reason. Good work.

[savannajolie]

Thanks for confirming aileen.

[sdelia10]

I had a really hard time setting this up. As soon as I opened the set up above it made sense and I got all the questions answered in under 2 minutes. When I first did this problem I spend over 6 minutes on set-up before giving up and moving on. Even after seeing the correct set-up I'm still perplexed as to how it was reached. Does any one have any tips, tricks or guidance on how to correctly identify and set up a grid like this? Thanks.

[aileenann]

So to begin with, this is an EXCEPTIONALLY difficult problem. MLSAT has gone back and forth a couple of times in our slides as to how to diagram the problem (check out session # 11 to see an MLSAT instructor discussing this problem).

That said, I think the important question is what do you do when you hit a really tough to diagram game? The key word is: flexibility. The LSAT is designed to put you in a tight spot and see how creative and resilient you are. So the best way to get rid of this is to actively seek out sort of kookie problems (for example the challenge games we publish every 2 weeks) and test yourself against them. Get used to adapting standard systems to unusual situations.

Sometimes there will be games that have no perfect diagram, that are some sort of hybrid. You need to know that even if your diagram isn't perfect from a strategic point of view, so long as it is accurate that will get you there. Never give up on a game once you've started it!

[interestedintacos]

I have been taking a look at this game and trying to draw lessons from it for the future. To me it seems like the main factor is that it has 3 variable sets. With that said, looking through the MLSAT Strategy Guide I found a good example of how to diagram it (page 220).

You diagram it the same way you would diagram an advanced linear game (I think you guys call it a 3D diagram), with the 6 loaves of bread as the base in linear order (although in reality there is no linear factor), and then the kinds of oatmeal and sliced/unsliced status above that lined up above.

It's exactly like game 3 in this practice test (PT 30), which also has 3 variable sets. The only difference is that in game 3 we are actually ordering, and it therefore the linear element of the diagram is actually active.

[ManhattanPrepLSAT1]

That's exactly right, good work! There's definitely more than one way to represent this game, but it's good to stick with something familiar, like the 3D Number Line, and then adapt it to whatever circumstances your facing.

Keep that in mind with the Open Board as well. We use that for open assignment games and it too is very adaptable to a diverse set of starting conditions.

[interestedintacos]

Plus, and as specified in the MLSAT guide, there are 2 types of open assignment games that can be very different: the matching games where repeats are allowed--which the guide focuses on (games where people often want to use a grid), and the games where repeats aren't allowed but are nevertheless "open" because we don't know exactly how many variables we are assigning to each group.

I think the open board works extremely well for the first category of games; it doesn't work as well for the other type. I don't know how often the other type shows up in the latest LSATs, but in the LSATs I'm working from now (1-38) it's showing up a lot.

For that open type the main consideration is often numerical distribution. There are usually only a few possible numerical distributions, and sometimes it's helpful to write those on the side, and that's more important than using the open board diagram method, although the open board can certainly work, so there's no harm in using it as a general strategy for both types of games.

There is one caveat I found though--if you don't recognize that a game falls into the second category and mistakenly think it's just like the first, then you are likely to use the wrong variable set as the base.

Other prep companies make the second category its own type of game: grouping distribution or something like that. It's more like a binary grouping game with more than 2 groups, and I've found so far that looking at the possible numerical distributions is really the key, and the open board won't really help but it can be a useful main diagram (as opposed to separate templates representing the numerical distributions or just a list of the possible numerical distributions).

Some games by the way are just binary grouping games masquerading as assignment games--like a couple games I've faced where the rules specify that each group will have either 3 or 4 members. So it's like a binary game with an extra twist because there is only one unfixed numerical distribution.

[monicaiannacone]

I'm struggling with the setup for this game. I read the response about someone posting a diagram but I don't see where a diagram is posted. Can someone post this diagram? This game took me too long as I struggled to find the correct setup. After just going with the rules, I got 3/5 correct but missed #3 and #4.

I don't see how 3D numbered ordering would work for these constraints since theres no ordering aspect. I thought this was closed assignment (exactly 6 loaves) but then it was undefined from there. I tried a setup with O, R, W as the base and U or S as the assignments. But this setup didn't work for #3 and #4 so I'm feeling pretty confused.

Thanks!

[mlbrandow]

I was able to solve this game in 3:23 using the setup above and a hypothetical for question 5.

I used ORW as a base because the only alternative is S/U/X (sliced, unsliced, not selected). I think you could do well with either, but I never tried with the latter.

On most games, there will be only a single question (the initial assignment question) which allows you to find the answer based on single rule violations alone.

What's atypical about this game as someone mentioned above is that, with the exception of Q5, every question is solvable from the initial rules, without need for application (hypothetical). Typically on a game there are multiple conditional questions, whereas this only features one (#5).

For question 3, (C) violates the initial diagram (rule 4) so it cannot be true.

For question 4, (D) must be true because there cannot be five (or six) sliced oatmeal loaves. There must be exactly six loaves selected, and rule 1 states that there must be at least two kinds of loaves. If there were five sliced loaves, combined with the one unsliced loaf (rule 4), then there could only be one kind (oatmeal).

Typically, when you get a global question (which of the following could/must/cannot be true?) you can potentially solve it in two ways: you can start constructing hypothetical diagrams, or you can check to see if one of the answer choices is in clear violation of an initial rule. In this game, the latter approach is able to knock out four of the five questions.

[timkim750]

Hey so there's an inherent ambiguity in question 3 that makes there to be 2 plausible answers. I already wrote to LSAC about it. Choice is the answer because it is in clear violation of rule 4 but I found choice A to be in violation of rule 5 as well. Choice A reads "The only unsliced loaves are oatmeal loaves." I interpreted this answer choice to mean a minimum of 2 loaves since the choice says "unsliced loaves" as opposed to there being only an unsliced loaf. If there are at least 2 unsliced loaves, then one of them must be rye. Clearly choice A violates that.

[ManhattanPrepLSAT1]

Hey so there's an inherent ambiguity in question 3 that makes there to be 2 plausible answers. I already wrote to LSAC about it. Choice is the answer because it is in clear violation of rule 4 but I found choice A to be in violation of rule 5 as well. Choice A reads "The only unsliced loaves are oatmeal loaves." I interpreted this answer choice to mean a minimum of 2 loaves since the choice says "unsliced loaves" as opposed to there being only an unsliced loaf.

I see your point! But I think that grammatically they're correct. When the quantity is unknown, and potentially plural (even though a single loaf is possible as well), the question should be phrased in plural.

Someone else chime in on this one if you can speak to the rules of English grammer, but I'd bet the LSAC looked that one up before they put it into a test that costs $1 million to produce.

Frustrating timkim750, I bet!

[ManhattanPrepLSAT1]

Here's our setup!

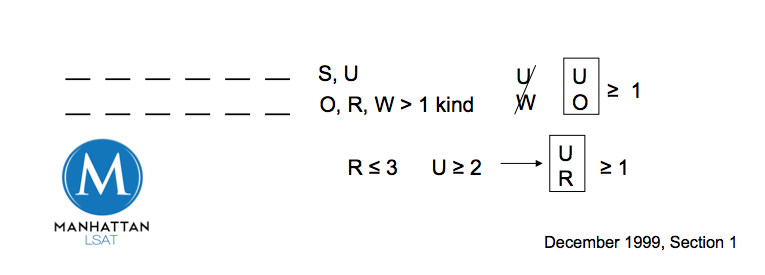
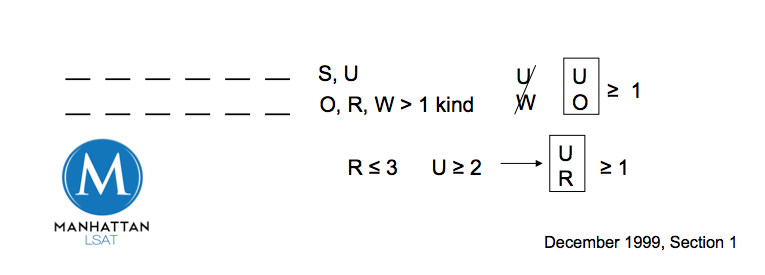
[bikramajit]

Hey so there's an inherent ambiguity in question 3 that makes there to be 2 plausible answers. I already wrote to LSAC about it. Choice is the answer because it is in clear violation of rule 4 but I found choice A to be in violation of rule 5 as well. Choice A reads "The only unsliced loaves are oatmeal loaves." I interpreted this answer choice to mean a minimum of 2 loaves since the choice says "unsliced loaves" as opposed to there being only an unsliced loaf.

I see your point! But I think that grammatically they're correct. When the quantity is unknown, and potentially plural (even though a single loaf is possible as well), the question should be phrased in plural.

Someone else chime in on this one if you can speak to the rules of English grammer, but I'd bet the LSAC looked that one up before they put it into a test that costs $1 million to produce.

Frustrating timkim750, I bet!

I agree with timkim750. The LSAC might have spent $ 1 million to produce this test but the Titanic cost even more and was supposed to be unsinkable ! The LSAC guys at Newtown are humans after all (believe me, they really are ) and they seem to have made a mistake here. And by the way, all those who allude to grammatical reasons to disprove ans choice A should realize that the LSAT is a test of Logic and not Grammar.

Did the LSAC reply to your query, timkim750 ? Please share if they did.

Or, can anyone else post an explanation based on logic and not grammar as to why A is incorrect ?

Thanks.

[ohthatpatrick]

LSAT is a test of logic, grammar, reading comprehension, critical thinking, common sense awareness of certain real world cause/effect structures, etc.

When LSAT gives a rule that says
Tom is before Mary and before Jen

we have to know grammar in order to understand that rule correctly
(someone missing the parallelism in "and" might otherwise think the rule is T - M - J)

Lawyers have to interpret the English language constantly, and doing so involves grammatical understanding (even if it's just an intuitive understanding of grammar).

If I say "some of the people who came to my party were Libertarians", how many people have I logically committed to?

At least one Libertarian at my party.

Some = "at least one"

So even though that sentence I gave involves plural nouns, the meaning of it still starts with a minimum of one.