The following relationship is what I got from the stimulus:(Please correct it if anything wrong.)
1. Tulip --> > Maple
some
2. Sycamores --> ~ >Maple
3. Maples --> Dogwoods
------------------------
The contrapositive of 1.
~>Maples --> ~ Tulip
To combine the above and 2.
some
Sycamores --> ~>Maples --> ~>Tulip
some
Sycamores --> ~>Tulip
So, it can be inferred that some sycamores are not as old as tulip trees. However, why is it true that some sycamores are not as old as "the youngest" tulip trees?
Could anyone explain it?
Thanks.
LSAT Forum
14 postsPage 1 of 1
-

- b91302310
-
Thanks Received: 13
-
Atticus Finch

- Posts: 153
- Joined: August 30th, 2010
-

- ManhattanPrepLSAT1
-
Thanks Received: 1909
-
Atticus Finch

- Posts: 2851
- Joined: October 07th, 2009
- This post thanked 2 times.
Re: Q12 - In the Centerville Botanical Gardens
I understand your desire to use conditional logic on this one, but I think it might be easier to work through if you treat this a mini-logic game.
Take a look at the follow diagram:
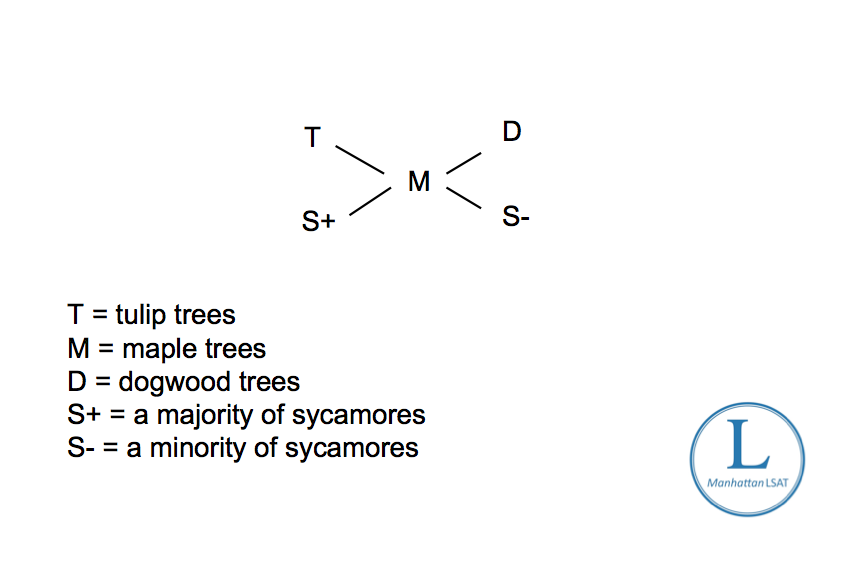
Let me know if you still have questions on this one, and if you would like to see another LR question just like this one, check out:
Feb96, S4, Q24 - In the Hartshorn Building
(you can find this in the SuperPrep published by the LSAC; PrepTest A, S4, Q24)
Take a look at the follow diagram:

Let me know if you still have questions on this one, and if you would like to see another LR question just like this one, check out:
Feb96, S4, Q24 - In the Hartshorn Building
(you can find this in the SuperPrep published by the LSAC; PrepTest A, S4, Q24)
-

- KakaJaja
-
Thanks Received: 1
- Forum Guests
- Posts: 37
- Joined: May 17th, 2012
Re: Q12 - In the Centerville Botanical Gardens
Thanks, the diagram is very clear. However, I don't understand why B is wrong? cuz some S are younger than M, and D are younger than M, so it is possible that some D are as old as the youngest S?
-

- nmop_apisdn2
-
Thanks Received: 16
-
Vinny Gambini

- Posts: 24
- Joined: June 23rd, 2012
- This post thanked 1 time.
Re: Q12 - In the Centerville Botanical Gardens
karenjiang2 Wrote:Thanks, the diagram is very clear. However, I don't understand why B is wrong? cuz some S are younger than M, and D are younger than M, so it is possible that some D are as old as the youngest S?
You basically talked about the answer to your own question.
If you are facing a must be true question and you find yourself thinking, "well, that could be true", or, "its possible", then you have not found the correct answer choice and you should move to a better one. You need to be able to say, "this must be true".
-

- ManhattanPrepLSAT1
-
Thanks Received: 1909
-
Atticus Finch

- Posts: 2851
- Joined: October 07th, 2009
Re: Q12 - In the Centerville Botanical Gardens
Exactly right nmop_apisdn2!
-

- slimjimsquinn
-
Thanks Received: 1
- Forum Guests
- Posts: 43
- Joined: February 11th, 2012
Re: Q12 - In the Centerville Botanical Gardens
I initially eliminated all of the answers, including the right one, E).
Why is e) correct but not d)?
d) some tulip trees are not as old as the oldest sycamore trees
- eliminated because we don't know the relationship between S and T. It belongs in the territory of 'we don't know'
e) some sycamores are not as old as the youngest tulip trees
- eliminated for the same reason - we don't know if this is true or not.
Can someone explain how e) is definitive? Is it because the terms are switched? If so, why does that make e) right?
Why is e) correct but not d)?
d) some tulip trees are not as old as the oldest sycamore trees
- eliminated because we don't know the relationship between S and T. It belongs in the territory of 'we don't know'
e) some sycamores are not as old as the youngest tulip trees
- eliminated for the same reason - we don't know if this is true or not.
Can someone explain how e) is definitive? Is it because the terms are switched? If so, why does that make e) right?
-

- timmydoeslsat
-
Thanks Received: 887
-
Atticus Finch

- Posts: 1136
- Joined: June 20th, 2011
- This post thanked 1 time.

- Most Thanked

- First Responder
Re: Q12 - In the Centerville Botanical Gardens
I wrote this down when I looked at the question:
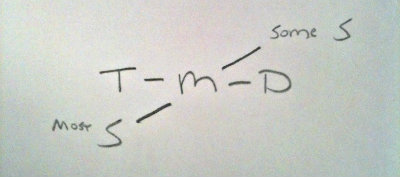
Notice that E must be true. We know that every single T is older than M. But we also know that there are some S's out there that are younger M.
So it must be true that some S's are not as old as even the youngest T in existence.
And with answer choice D, like you said, we do not know the relationship of the "most S" group to the T group. We do have a specified relationship between the T group and the "some S" group.
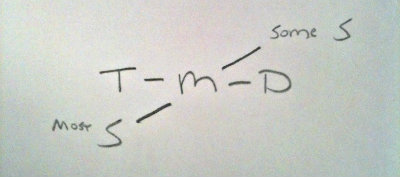
Notice that E must be true. We know that every single T is older than M. But we also know that there are some S's out there that are younger M.
So it must be true that some S's are not as old as even the youngest T in existence.
And with answer choice D, like you said, we do not know the relationship of the "most S" group to the T group. We do have a specified relationship between the T group and the "some S" group.
-

- monygg85
-
Thanks Received: 1
-
Jackie Chiles

- Posts: 29
- Joined: December 04th, 2012
Re: Q12 - In the Centerville Botanical Gardens
So I stumbled on this question while practicing MBT. This is a very strange question to me in terms of diagramming. Especially now with seeing the diagrams used by previous posters, they are unlike other conditional diagrams in MBT.
Are there any other questions like this for me to practice? This would stump me during the test...I mean how did you guys know to diagram it out differently rather than use conditionals which is what I intuitively started to do but quickly realized it was a mess.
Are there any other questions like this for me to practice? This would stump me during the test...I mean how did you guys know to diagram it out differently rather than use conditionals which is what I intuitively started to do but quickly realized it was a mess.
-

- ban2110
-
Thanks Received: 0
-
Jackie Chiles

- Posts: 31
- Joined: August 18th, 2012

- Most Thankful
Re: Q12 - In the Centerville Botanical Gardens
monygg85 Wrote:So I stumbled on this question while practicing MBT. This is a very strange question to me in terms of diagramming. Especially now with seeing the diagrams used by previous posters, they are unlike other conditional diagrams in MBT.
Are there any other questions like this for me to practice? This would stump me during the test...I mean how did you guys know to diagram it out differently rather than use conditionals which is what I intuitively started to do but quickly realized it was a mess.
I can't speak for how anyone else, but what tipped me off was the stimulus; it reminded me immediately of a linear logic game, since those tend to feature "ordering" conditions.
-

- redcobra21
-
Thanks Received: 4
-
Elle Woods

- Posts: 59
- Joined: July 16th, 2013
Re: Q12 - In the Centerville Botanical Gardens
That is a great idea to treat this like a logic game. Two questions: (1) Are there any other instances in previous LSATs where you had to adopt such an approach? (2) Would this be possible to solve using conditional logic?
I bring up (2) since I had never approached any LR like a LG and was wondering if it would be possible to solve this problem if I had not made that realization
I bring up (2) since I had never approached any LR like a LG and was wondering if it would be possible to solve this problem if I had not made that realization
-

- nandy_millette
-
Thanks Received: 2
-
Vinny Gambini

- Posts: 25
- Joined: March 09th, 2013
Re: Q12 - In the Centerville Botanical Gardens
redcobra21 Wrote:(2) Would this be possible to solve using conditional logic?
I got this answer right using conditional logic and some formal logic so maybe it is possible (if my reasoning is right)
TT= tulip tree
OTM=older than maples
S=sycamores
M=maples
OTDW=older than dogwoods
1) TT-->OTM
~OTM-->~TT
2)Majority (but not all) S are OTM
Some S are ~OTM
3) M-->OTDW
~OTDW-->~M
From my diagrams/statements above I was able to infer two statements that must be true:
a)All TT are OTDW (combination of "All" statement in 1) and "All" statement in 3)
b)Some S are OTDW (combination of "Most" statement in 2) and "All" statement in 3)
My first step was to look for my paraphrase but I did not see it, I then compared all of the answer choices to my statements above and eliminated the answer choices that could not be inferred, Answer choice E) was the only one that could be inferred based on the statements.
I recognize that the use of the diagram is more efficient but in an exam I would not think of using such a diagram and would stick to what I know (I am working on being less rigid when answering LR questions)
So is my reasoning wrong?
-

- tangdanni422
-
Thanks Received: 7
-
Vinny Gambini

- Posts: 12
- Joined: April 14th, 2014
Re: Q12 - In the Centerville Botanical Gardens
Hey guys, I have read the above posts but I have two questions...
1. Why the minority of sycamores has to be younger than ANY of maples. Could it possible that all these minority of sycamores are AS OLD AS maples? I read the stimulus and it suggests that the minority of sycamores does not have to be younger than ANY of maples... What am I missing?
So it could be diagramed like:
Tulips & Majority of S > Maples & Minority of S > Dogwoods
2. I understand why (e) is right but what is wrong with (c)? Those majority of sycamores are not as old as the oldest dogwoods.
1. Why the minority of sycamores has to be younger than ANY of maples. Could it possible that all these minority of sycamores are AS OLD AS maples? I read the stimulus and it suggests that the minority of sycamores does not have to be younger than ANY of maples... What am I missing?
So it could be diagramed like:
Tulips & Majority of S > Maples & Minority of S > Dogwoods
2. I understand why (e) is right but what is wrong with (c)? Those majority of sycamores are not as old as the oldest dogwoods.
-

- dangilomartin
-
Thanks Received: 0
-
Vinny Gambini

- Posts: 5
- Joined: July 24th, 2014
Re: Q12 - In the Centerville Botanical Gardens
I have read all the post and I am still at a lose. I just don't understand what is going on in this passage.
I clearly see that the first and the third rule link up.
T---->M---->D
The second rule however seems to me to be as follows
Most S----> ~M (the not M) because it explicitly says NOT All)
I don't understand how you can connect this to the "M" in the super rule. That M is a positive this M is a negative. Plus I was told there are no contrapostives of MOST or Some relationships. Please help.
I clearly see that the first and the third rule link up.
T---->M---->D
The second rule however seems to me to be as follows
Most S----> ~M (the not M) because it explicitly says NOT All)
I don't understand how you can connect this to the "M" in the super rule. That M is a positive this M is a negative. Plus I was told there are no contrapostives of MOST or Some relationships. Please help.
-

- ohthatpatrick
-
Thanks Received: 3808
-
Atticus Finch

- Posts: 4661
- Joined: April 01st, 2011
- This post thanked 2 times.
Re: Q12 - In the Centerville Botanical Gardens
It’s a little weird to diagram this conditionally, because conditional ideas are binary YES/NO ideas, but these are OLDER/YOUNGER. That’s why people converted to an ordering mindset.
If we want to do this conditionally, we have to basically make an arbitrary decision on YES meaning “older” or “younger”.
Let’s say YES = OLDER
How do we write the first sentence?
T —> M ?
How do I read that? “If T is older, then M is older?”
Should I write
T —> ~M ?
“If T is older, then M is younger”?
These both seem unworkable to me because T is older. There’s no “if” to it.
Conditional ideas can also be thought of as “All A are B” or “A requires B”, etc., but none of those fit either.
All tulips are maples? Being a tulip requires being a maple?
Unfortunately, conditional logic isn't well suited for this problem, especially given the continuum nature of the answer choices. Again, binary logic ain't a good match for the fluidity of a timeline.
The first and last sentence chain together intuitively in a chronological order.
All tulips, then all maples, then all dogwoods. No overlap or ambiguity with their timeline.
This eliminates
(A) D’s and T’s never overlap.
In terms of those pesky sycamores, MOST of them are older than any maples. SOME of them are younger that the maples.
Given that all the answer choices are in "some" format, the fact that MOST are pre-maple is really irrelevant.
The key idea is just that Some S's are pre-maple, some S's are post-maple (technically, those S's could be concurrent with maple, but for simplicity's sake, we'll say post-maple).
We might ask ourselves about the pre-maple S's ...
How much before? Are they before the tulips? Contemporaneous with the tulips? After the tulips but before the maples? All of the above?
Who knows? Any of those could be true.
What about the Sycamores that come in the post-Maple era? Are they contemporaneous with the maples? Are they after the Maple-era but before the Dogwood era? Are they after the Dogwood era? Are they all three?
Who knows? Any of those could be true.
All we know that MUST be true hinges on the fact that we know SOME sycamores came before the Maple era, and SOME came during/after it.
We know that sycamores that came before the Maple era also came before the Dogwood era, because the Maple era ended before the Dogwood era began.
We know that sycamores that came during/after the Maple era came after the Tulip era, because the Tulip era ended before the Maple era began.
(B) This is dealing with the "who knows" part of the post-Maple sycamores. To show this doesn't HAVE to be true, consider this possible timeline:
TTT - SS - MMM - S - DDD
Here, even the YOUNGEST dogwood is still older than the OLDEST sycamore.
(C) Clean this up as "some S's are younger than the oldest D's". The same timeline shows how this could be false.
TTT - SS - MMM - S - DDD
Here, ALL the sycamores are older than any dogwood.
(D) This deals with the "who knows" part of the pre-Maple sycamores. The same timeline shows how this could be false.
TTT - SS - MMM - S - DDD
Here, ALL the tulip trees are older than any sycamore.
(E) Correct answer. Clean it up as "some S's are younger than than the youngest T's".
Sure, that's part of what we originally deduced:
the post-maple S's are all younger than the T's.
the pre-maple S's are all older than the D's.
Since there MUST be an S that comes after all the M's, and the M's come after all the T's, there must be an S that comes after all the T's. Hence, there must be an S that is younger than all the T's.
In regards to a previous poster's questions about other questions like this, I can't think of any. There are a couple Inference questions that test quantitative continuum relationships. Here's the one that comes to my mind:
PT47, Sec1, Q18
If we want to do this conditionally, we have to basically make an arbitrary decision on YES meaning “older” or “younger”.
Let’s say YES = OLDER
How do we write the first sentence?
T —> M ?
How do I read that? “If T is older, then M is older?”
Should I write
T —> ~M ?
“If T is older, then M is younger”?
These both seem unworkable to me because T is older. There’s no “if” to it.
Conditional ideas can also be thought of as “All A are B” or “A requires B”, etc., but none of those fit either.
All tulips are maples? Being a tulip requires being a maple?
Unfortunately, conditional logic isn't well suited for this problem, especially given the continuum nature of the answer choices. Again, binary logic ain't a good match for the fluidity of a timeline.
The first and last sentence chain together intuitively in a chronological order.
All tulips, then all maples, then all dogwoods. No overlap or ambiguity with their timeline.
This eliminates
(A) D’s and T’s never overlap.
In terms of those pesky sycamores, MOST of them are older than any maples. SOME of them are younger that the maples.
Given that all the answer choices are in "some" format, the fact that MOST are pre-maple is really irrelevant.
The key idea is just that Some S's are pre-maple, some S's are post-maple (technically, those S's could be concurrent with maple, but for simplicity's sake, we'll say post-maple).
We might ask ourselves about the pre-maple S's ...
How much before? Are they before the tulips? Contemporaneous with the tulips? After the tulips but before the maples? All of the above?
Who knows? Any of those could be true.
What about the Sycamores that come in the post-Maple era? Are they contemporaneous with the maples? Are they after the Maple-era but before the Dogwood era? Are they after the Dogwood era? Are they all three?
Who knows? Any of those could be true.
All we know that MUST be true hinges on the fact that we know SOME sycamores came before the Maple era, and SOME came during/after it.
We know that sycamores that came before the Maple era also came before the Dogwood era, because the Maple era ended before the Dogwood era began.
We know that sycamores that came during/after the Maple era came after the Tulip era, because the Tulip era ended before the Maple era began.
(B) This is dealing with the "who knows" part of the post-Maple sycamores. To show this doesn't HAVE to be true, consider this possible timeline:
TTT - SS - MMM - S - DDD
Here, even the YOUNGEST dogwood is still older than the OLDEST sycamore.
(C) Clean this up as "some S's are younger than the oldest D's". The same timeline shows how this could be false.
TTT - SS - MMM - S - DDD
Here, ALL the sycamores are older than any dogwood.
(D) This deals with the "who knows" part of the pre-Maple sycamores. The same timeline shows how this could be false.
TTT - SS - MMM - S - DDD
Here, ALL the tulip trees are older than any sycamore.
(E) Correct answer. Clean it up as "some S's are younger than than the youngest T's".
Sure, that's part of what we originally deduced:
the post-maple S's are all younger than the T's.
the pre-maple S's are all older than the D's.
Since there MUST be an S that comes after all the M's, and the M's come after all the T's, there must be an S that comes after all the T's. Hence, there must be an S that is younger than all the T's.
In regards to a previous poster's questions about other questions like this, I can't think of any. There are a couple Inference questions that test quantitative continuum relationships. Here's the one that comes to my mind:
PT47, Sec1, Q18
14 posts Page 1 of 1