Hello
Could someone please provide explanations for Q 6,7,and 11 please?
LSAT Forum
2 postsPage 1 of 1
-

- timmydoeslsat
-
Thanks Received: 887
-
Atticus Finch

- Posts: 1136
- Joined: June 20th, 2011

- Most Thanked

- First Responder
Re: Q6
This is a sequencing game with six variables.
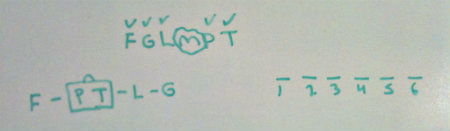
This is what my global diagram looks like.
The only question this game offers is where to place M, other than the rotating block of PT.
Question 6 is just a partial hypothetical lineup. You should treat it no differently than any other general first logic game question in which you hunt for a single valid hypothetical. Take a rule, apply it to each answer choice, and repeat this until only one choice is left.
A)
B) G could never be first.
C) L must be before F.
D) T must be next to P.
E) F must go before T and P.
A wins by default.
Question 7 is a global question asking what cannot be fourth.
This can be answered by looking at our global diagram. I would immediately look to the extremes of the chain. F couldnt be fourth, as only two spots come after fourth, and F has four variables come after it. Also, G could never be fourth, as it has four variables come before it, which means the soonest G could go is fifth.
The testwriters made G the choice for this one (A).
Question 11 is a local question asking what must be false. Our local information is that P is immediately next to L. This would require us to have a TPL block, as there is no other way for P to be next to both L and T in this sequence. So we now have this:
F - TPL - G
And our random variable of M.
A) Sure F could be 2, M could be first to make this happen.
B) Sure P could be 4, M could be second to make this happen.
C) No way. How can make T fourth? Only way to even attempt it is to supply the left side of the sequence chain with more variables to make F fourth. The only variable we can plug in there is M, so now we have T going third, but never fourth. Every other variable is forced in their respective place.
D) G can be 5 by making M last.
E) M can be 5 by placing M right after L and before G.
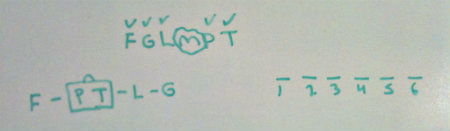
This is what my global diagram looks like.
The only question this game offers is where to place M, other than the rotating block of PT.
Question 6 is just a partial hypothetical lineup. You should treat it no differently than any other general first logic game question in which you hunt for a single valid hypothetical. Take a rule, apply it to each answer choice, and repeat this until only one choice is left.
A)
B) G could never be first.
C) L must be before F.
D) T must be next to P.
E) F must go before T and P.
A wins by default.
Question 7 is a global question asking what cannot be fourth.
This can be answered by looking at our global diagram. I would immediately look to the extremes of the chain. F couldnt be fourth, as only two spots come after fourth, and F has four variables come after it. Also, G could never be fourth, as it has four variables come before it, which means the soonest G could go is fifth.
The testwriters made G the choice for this one (A).
Question 11 is a local question asking what must be false. Our local information is that P is immediately next to L. This would require us to have a TPL block, as there is no other way for P to be next to both L and T in this sequence. So we now have this:
F - TPL - G
And our random variable of M.
A) Sure F could be 2, M could be first to make this happen.
B) Sure P could be 4, M could be second to make this happen.
C) No way. How can make T fourth? Only way to even attempt it is to supply the left side of the sequence chain with more variables to make F fourth. The only variable we can plug in there is M, so now we have T going third, but never fourth. Every other variable is forced in their respective place.
D) G can be 5 by making M last.
E) M can be 5 by placing M right after L and before G.
2 posts Page 1 of 1
