Q9

[timmydoeslsat]

I received a question about #9 and I wanted to post my technique for answering this question.

This is a local question asking us for what could be true.

We are given the additional information of 2 windows having exactly 2 colors.

We are asked what could be the 2 colors in one of those windows.

Well, either the GP block is in this combination of exactly 2 or it is not.

I show this in this local diagram:



I also know from the rules that each glass must contain at least one of P and O. I will eliminate any answer choice that violates this constraint. And I will also be on the lookout for things like Y being with either G or O.

I am able to eliminate A and D for violating the ~P ---> O rule.

I am down to B, C, E.

You could choose to plug in these answer choices and see if you can make a hypothetical work, as this is just a could be true question stem.

I will go with my initial local diagram and make inferences.

I will go with my first frame, the one with GP being part of the 2 color glass group. This will require that R be present in both of the 2nd and 3rd windows.



One of these windows must contain exactly 2 slots. I also know that each window contains at least one of P/O. This means that the third window in my setup must contain the Y, which would require the P. I know that at least one of P/O must be present in each window, thus Y must be with P since Y precludes O (and G).



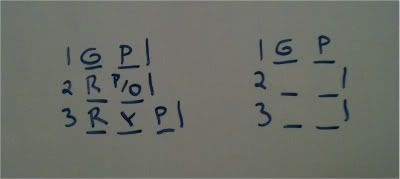
This completes the third window. No other options can happen. I have not placed the O definitely, which means that I must change that dual option from O/P to an O. Every color must be used at least once.

So this does show us that R and O can be one of those windows with exactly 2 colors in them.



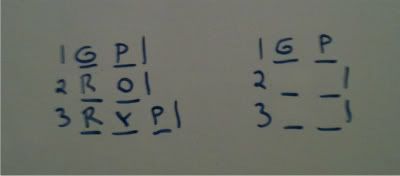
That was the frame concerning GP being included in the idea of 2 windows having exactly 2 colors.

The other frame will show GP not being included in the idea of 2 windows having exactly 2 colors.

This idea requires that the other 2 windows have exactly 2 windows.

We also know that at least one of these windows must contain an R.



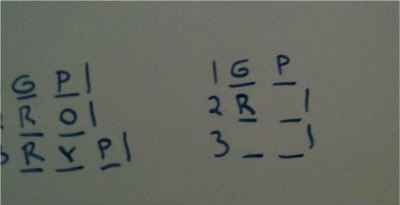
We don't know as of right now whether the R would go in the 3rd window or the 1st with the GP block. That is until we consider where Y can do. It cannot go in block 2, as we know we are really placed a YP block. The only place it can go is window 3, so that is where it must go since all colors must be used at least once. I also know that the other variable in window 2 must be one of P/O due to the rules.



This will now force the other R into window 1.

That is what is certain for this scenario.



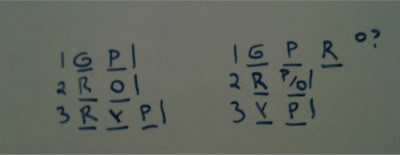
We can have O be in window 1. If O is not in window 1, then window 2 must contain the O rather than the dual option, as each color must be used at least once.

[at9037]

I can't seem to understand why can't C and E be the answer?

[christine.defenbaugh]

timmydoeslsat does a great job above of walking through how to arrive at answer choice (B) positively, showing the O+R could be a window that has exactly two colors, under the constraints.

If we were doing plug-n-chug, though, we'd be instead looking to verify why all the other answer choices cannot work.

For (C): If O+P made up one of the 2-color windows, then we'd have to stick the two R's in the other two windows (as they have to go somewhere!

We know that the GP chunk must go somewhere (other than the first window):

We also know that Y must end up somewhere, and only the middle window will allow it now:

Wherever Y goes, P must follow, and thus we have violated the condition of the question (that two windows have exactly 2 colors):


For (E), we have a similar problem: If O+G made up one of the 2-color windows, then we'd have to stick the two R's in the other two windows (as they have to go somewhere!

We know that the GP chunk must go somewhere (other than the first window):

We also know that Y must end up somewhere, and only the middle window will allow it now:

Wherever Y goes, P must follow, and thus we have violated the condition of the question (that two windows have exactly 2 colors):


Both answer choices end up failing on plug-n-chug, for almost identical reasons.

Does that help clear things up a bit?